0÷0 と 0/0

𝑎, 𝑏 を変数とする。

左分配法則より、下記かきの等式が成なり立たつ。

(𝑎×𝑏)−(𝑎×𝑏) = 𝑎×(𝑏−𝑏)

元の数と取り除く数が等しいときの差は0なので、下記の等式が成り立つ。

0 = 𝑎×0

つまり、0倍ばいすればどんな数でも0になってしまう。

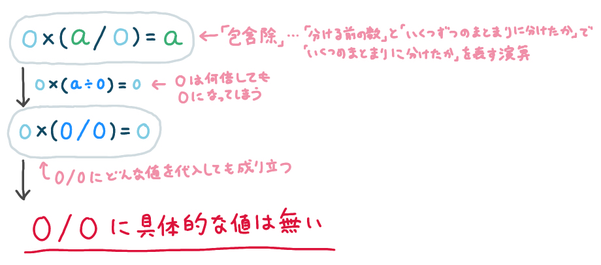
0倍されたらどんな数でも0になるので、𝑎÷0 の 𝑎 に代入できる値は0しかない。

さらに、0÷0 にはどんな値でも代入できてしまうので、この数式に具体的ぐたいてきな値は無ない。

右分配法則より、下記の等式が成り立つ。

(𝑎−𝑎)×𝑏 = (𝑎×𝑏)−(𝑎×𝑏)

元の数と取り除く数が等しいときの差は0なので、下記の等式が成り立つ。

0×𝑏 = 0

つまり、0を何なん倍しても0になってしまう。