乗法の結合法則

𝑎, 𝑏, 𝑐 を変数とする。

積 𝑎×𝑏 を 𝑐 倍ばいすると、分わけることができる 𝑎 ずつのまとまりの数も 𝑐 倍になるので、下記かきの等式が成なり立たつ。

(𝑎×𝑏)×𝑐 = 𝑎×(𝑏×𝑐)

このことを、乗法の結合法則(associative law)という。

「分けることができるまとまりの数」というのはつまり割合のことであり、積は「分ける前まえの数」のことなので、

割合 𝑎/𝑏 を 𝑐 倍すると、分ける前の数も 𝑐 倍になるので、下記の等式が成り立つ。

(𝑎/𝑏)×𝑐 = (𝑎×𝑐)/𝑏

積を 𝑐 倍すると割合も 𝑐 倍になるが、このとき、「いくつずつに分けたか」、つまり商は変かわっていない。

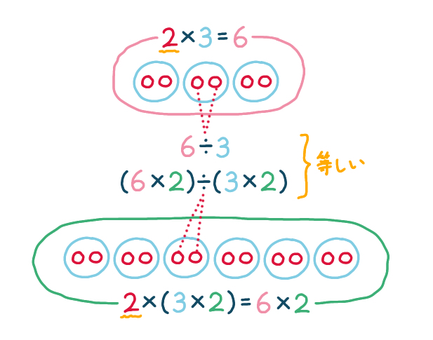
なので、下記の等式も成り立つ。

𝑎÷𝑏 = (𝑎×𝑐)÷(𝑏×𝑐)