分配法則

𝑎, 𝑏, 𝑐 を変数とする。

積 𝑎×𝑏 に 𝑎 ずつのまとまりをいくつか加くわえると、分わけることができる 𝑎 ずつのまとまりの数がその分ぶん増ふえるので、下記かきの等式が成なり立たつ。

(𝑎×𝑏)+(𝑎×𝑐) = 𝑎×(𝑏+𝑐)

このことを、左分配法則ひだりぶんぱいほうそく (left distributive law)という。

さらに、𝑏 に 𝑏−𝑐 を代入する。

(𝑎×(𝑏−𝑐))+(𝑎×𝑐) = 𝑎×((𝑏−𝑐)+𝑐)

(𝑏−𝑐)+𝑐 = 𝑏 なので、下記の等式が成り立つ。

(𝑎×(𝑏−𝑐))+(𝑎×𝑐) = 𝑎×𝑏

減法は加法の逆演算なので、下記の等式が成り立つ。

(𝑎×𝑏)−(𝑎×𝑐) = 𝑎×(𝑏−𝑐)

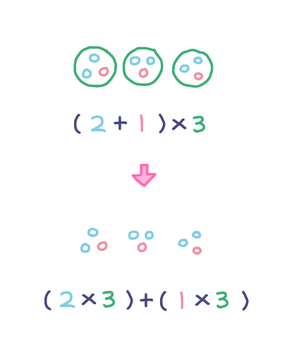
和 𝑎+𝑏 を 𝑐 倍ばいすると、𝑎 ずつのまとまりの数と 𝑏 ずつのまとまりの数が 𝑐 になるので、下記の等式が成り立つ。

(𝑎+𝑏)×𝑐 = (𝑎×𝑐)+(𝑏×𝑐)

このことを、右分配法則みぎぶんぱいほうそく(right distributive law)という。

さらに、𝑎 に 𝑎−𝑏 を代入する。

((𝑎−𝑏)+𝑏)×𝑐 = ((𝑎−𝑏)×𝑐)+(𝑏×𝑐)

(𝑎−𝑏)+𝑏 = 𝑎 なので、下記の等式が成り立つ。

𝑎×𝑐 = ((𝑎−𝑏)×𝑐)+(𝑏×𝑐)

減法は加法の逆演算なので、下記の等式が成り立つ。

(𝑎−𝑏)×𝑐 = (𝑎×𝑐)−(𝑏×𝑐)

左分配法則・・・・や右分配法則・・・・のことを分配法則ぶんぱいほうそく(distributive law)という。